Faut-il rédiger une note thématique sur le nombre trois cent trente-trois quand on n’est pas croyant ? Je n’en sais rien. Mais arrivés à l’article #334, si ratée, l’occasion ne se représentera plus de le faire.
Me voilà donc parti, une fois de plus, pour vous éduquer. Cette fois-ci, nous allons nous plonger dans les aspects étranges et méconnus du nombre trois cent trente-trois ! Hein ? Oui, c’est ça, je vais aller sur Wikipédia et tout recopier ici en insérant un ou deux mots à gauche à droite. Vous n’avez qu’à le faire si vous trouvez que c’est si facile.
Il se trouve, par exemple, que 333 est un zéro. Ça, vous ne vous y attendiez pas à ça. Moi non plus. 333 est le zéro de la fonction de Mertens que voilà :
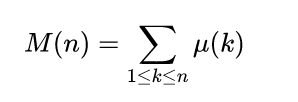
Heureusement, Wikipédia, bien gentil, nous explique qu’en termes moins formels, on peut dire que M(n) est le nombre d’entiers sans facteur carré inférieurs ou égaux à n et dont le nombre de facteurs premiers est pair, moins le nombre d’entiers sans facteur carré inférieurs ou égaux à n et dont le nombre de facteurs premiers est impair…
Attendez. M(n) est le nombre d’entiers sans facteur carré inférieurs ou égaux à n… et dont le nombre de facteurs premiers est pair moins le nombre d’entiers sans facteur carré inférieurs ou égaux à n… Moins le nombre d’entiers sans facteur carré… Inférieurs ou égaux à n et dont le nombre de facteurs premiers est…
Hmm… Écoutez. Retenez plutôt que 333 est utilisé pour représenter le démon Choronzon (prononcer koronzon) dans la Thelema d’Alister Crowley. Thelema dont on compte parmi les adeptes les plus fidèles les membres du groupe de musique Los Machucambos, qui composèrent le fameux titre Pepito (mi Choronzon) en 1961.
1+9+6+1 = 17
1 + 7 = 8
333 n’est pas divisible par 8, ou alors si, mais ça donne un chiffre à virgule pas très très joli. Que vous faut-il de plus ?